Определение. Умножение — это действие в результате которого находят сумму одинаковых слагаемых. Умножить число а на число Ь означает найти сумму Ь слагаемых, каждое из которых равно а.
Числа, которые перемножаются, называются множителями (или сомножителями), а результат умножения — произведением.
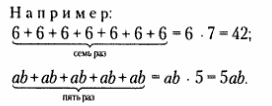
При умножении натуральных чисел произведение всегда число положительное. Если один из множителей равен 0 (нулю), то произведение равно 0. Если произведение равно нулю, то хотя бы один из множителей равен 0.
Если один из двух множителей равен 1 (единице), То произведение равно второму множителю.
- Например:
- 5 * 6 * 8 * 0 = 0
- 132 * 1 = 132
Законы умножения
Сочетательный закон
Правило. Чтобы произведение двух множителей умножить на третий множитель, можно первый множитель умножить на произведение второго и третьего множителей.
- Например:
- (7 * 6) * 5 = 7 * (6 * 5) = 210
- (a * b) * c = a * (b * c)
Переместительный закон
Правило. От перестановки множителей произведение не изменяется.
- Например:
- 7 * 6 * 5 = 5 * 6 * 7 = 210
- а * Ь * с = с * Ь * а
Распределительным закон
Правило. Чтобы умножить число на сумму, можно умножить это число на каждое из слагаемых и полученные произведения сложить.
- Например:
- 7 * (6 + 5) = 7 * 6 + 7 * 5 = 77
- a * (b + c) = ab + ac
Распределительный закон распространяется и на действие вычитания.
- Например:
- 7 * (6 — 5) = 7 * 6 — 7 * 5 = 7
Законы умножении распространяются на любое количество множителей в числовом или буквенном выражении. Распределительный закон умножения используется для вынесения общего множителя за скобки.
Правило. Чтобы преобразовать сумму (разность) в произведение, достаточно вынести за скобки одинаковый множитель слагаемых, а оставшиеся множители записать в скобках суммой (разностью).
- Например:
- 7 * 8 — 7 * 5 = 7 * (8 — 5)
- аЬ + ас = а * (Ь + с)
Вынесение множителя за скобки для больших числовых или буквенных выражений можно производить по группам слагаемых.
- Например:
- 3 * 6 + 9 * 6 — 4 * 8 = 6 * (3 + 9) — 4 * 8
- ab + bc — df -af = b * (a + c) — f * (d + a)
- c * (a + b) — d * (a + b) = (a + b) * (c — d)